Our group has discovered a striking similarity between theories of physics and more general models used to study complex systems such as in systems biology, economics, ecology, climate science, etc.
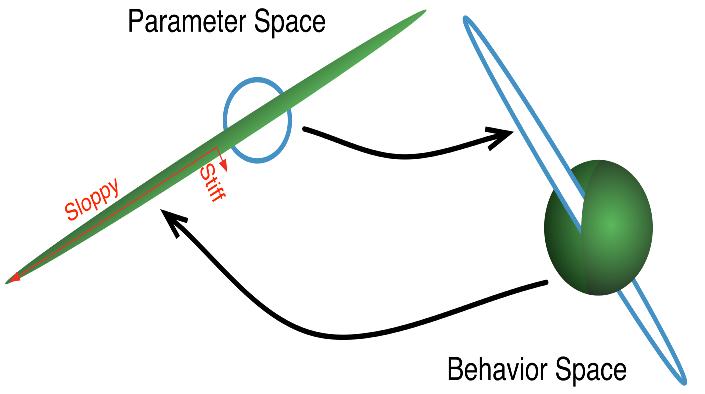
Over the past decade, we have been studying a wonderful commonality in these more general systems. Their collective behavior depends mostly on a few "stiff' combinations of rules; most other combinations are sloppy, with little or no influence on system behavior.

|
| Sloppy models are multiparameter models, whose behavior depends only on a few stiff combinations of parameters, with many sloppy parameter directions largely unimportant for model predictions. We've found them ubiquitous in systems biology and in other fields of science where models are fit to data. |

|
| Hyperribbon structure in behavior space, for the diffusion equation after three evolution steps. Note that it is longer than it is wide, and it is very thin -- like a ribbon. |
Indeed, theoretical physics is like a tree (figures below). Our
high-energy colleagues study the limbs of the tree, searching for more
unified theories closer to the trunk. We in condensed matter physics build
outward, searching for 'emergent' branches and leaves -- effective theories
describing sound, semiconductors, and superfluids.
Does physics share the 'sloppy model' behavior we found in other sciences?
We generalized our information geometry methods and applied them to
two standard physics models -- diffusion and the Ising model (figure at left).
The diffusion equation describes how perfume goes from her skin
to your nose (if the air is still). It is usually derived as a continuum
limit, using methods similar to those we use for describing many other
phases and phenomena in condensed matter physics -- sound, magnets, and
superconductors. The Ising model of magnetism, which becomes fractal,
is usually analyzed using renormalization group
similar to methods used in high-energy physics. Our method, different
from continuum limits and renormalization group methods, examines
different combinations of the microscopic rules, finding the stiff and sloppy
directions. The figure at left shows that the diffusion equation and the
Ising model share the same spread of stiff and sloppy combinations as do
systems drawn from other branches of science. Moreover, the stiff directions
directly correspond to the important combinations that the traditional
continuum limit and renormalization-group methods identified as the
collective, emergent control parameters.
If one needed to extract every detail of the true underlying theory to make
a useful theory, science would be impossible. Sloppiness makes science possible.
James P. Sethna, sethna@lassp.cornell.edu; This work supported by the Division of Materials Research of the U.S. National Science Foundation, through grant DMR-1005479.
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).